Fireblocks Tokenization Platform
Asset tokenization platform for the future of digital financial markets
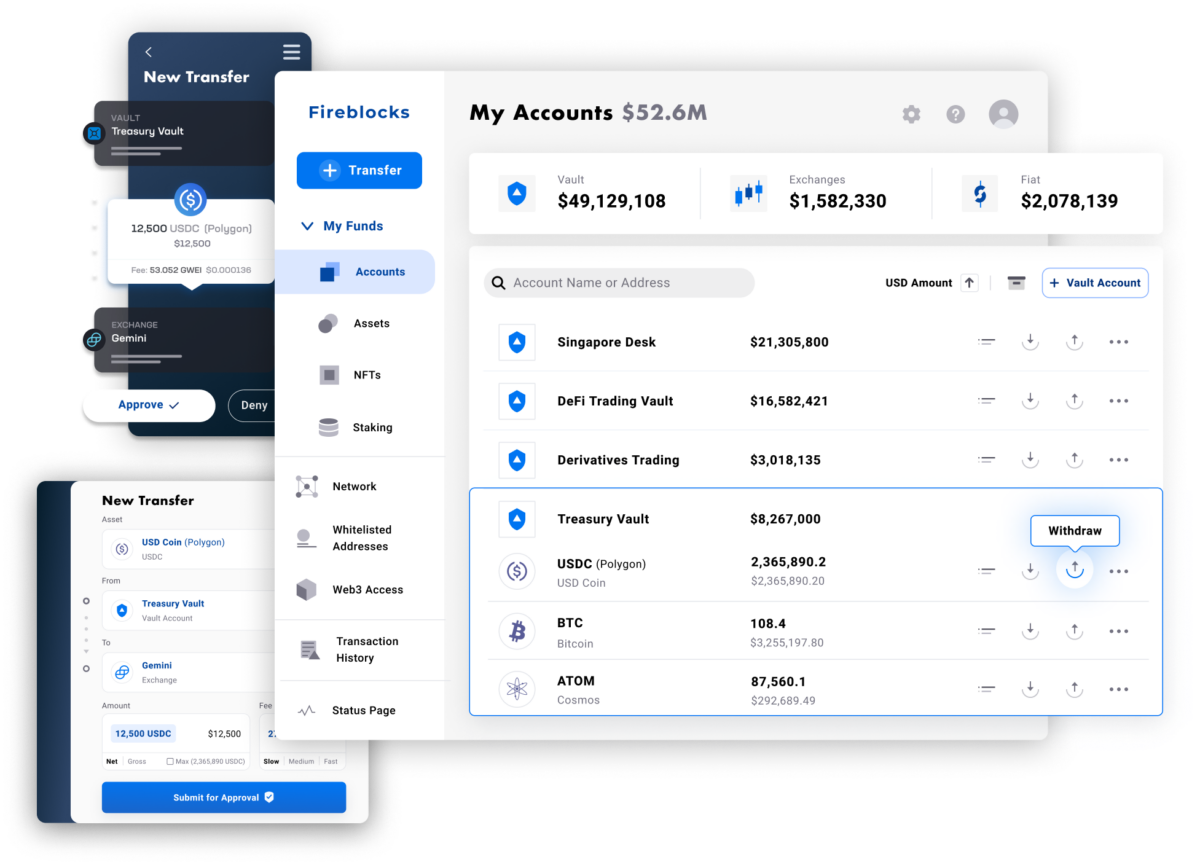
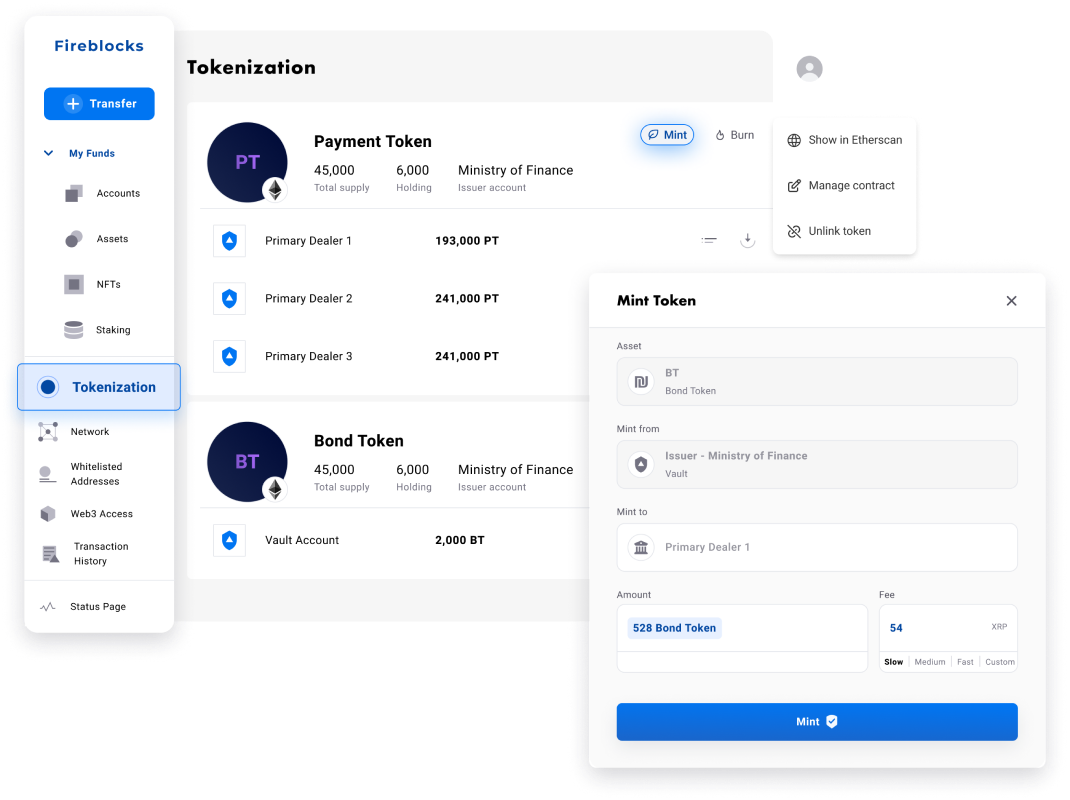
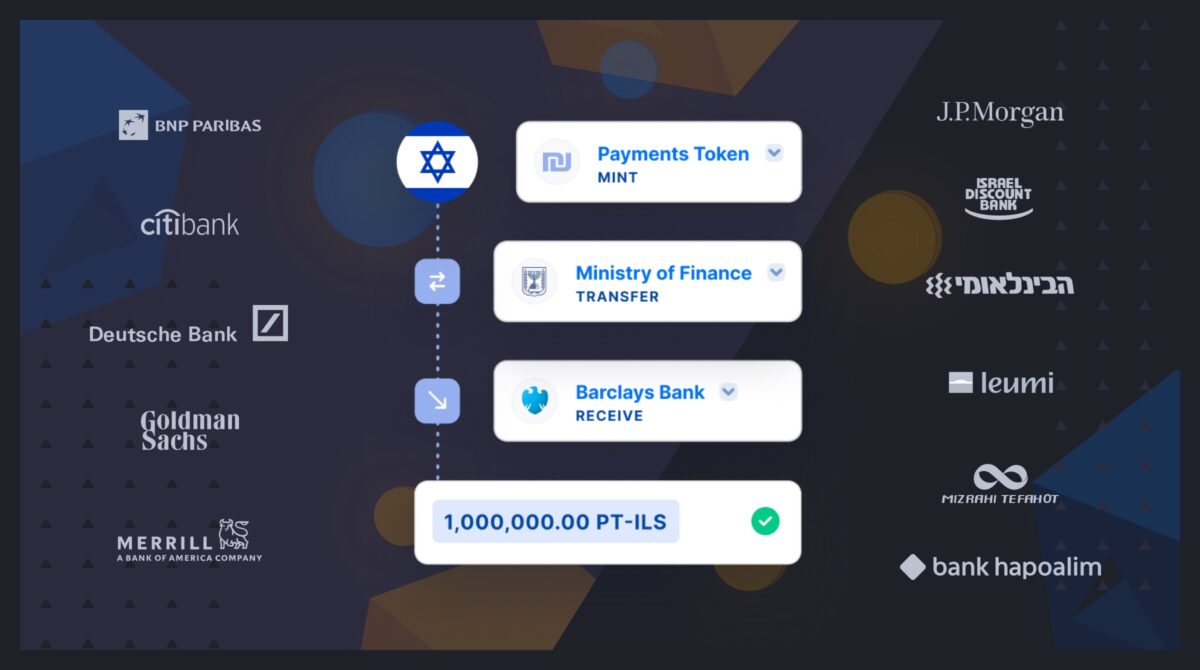
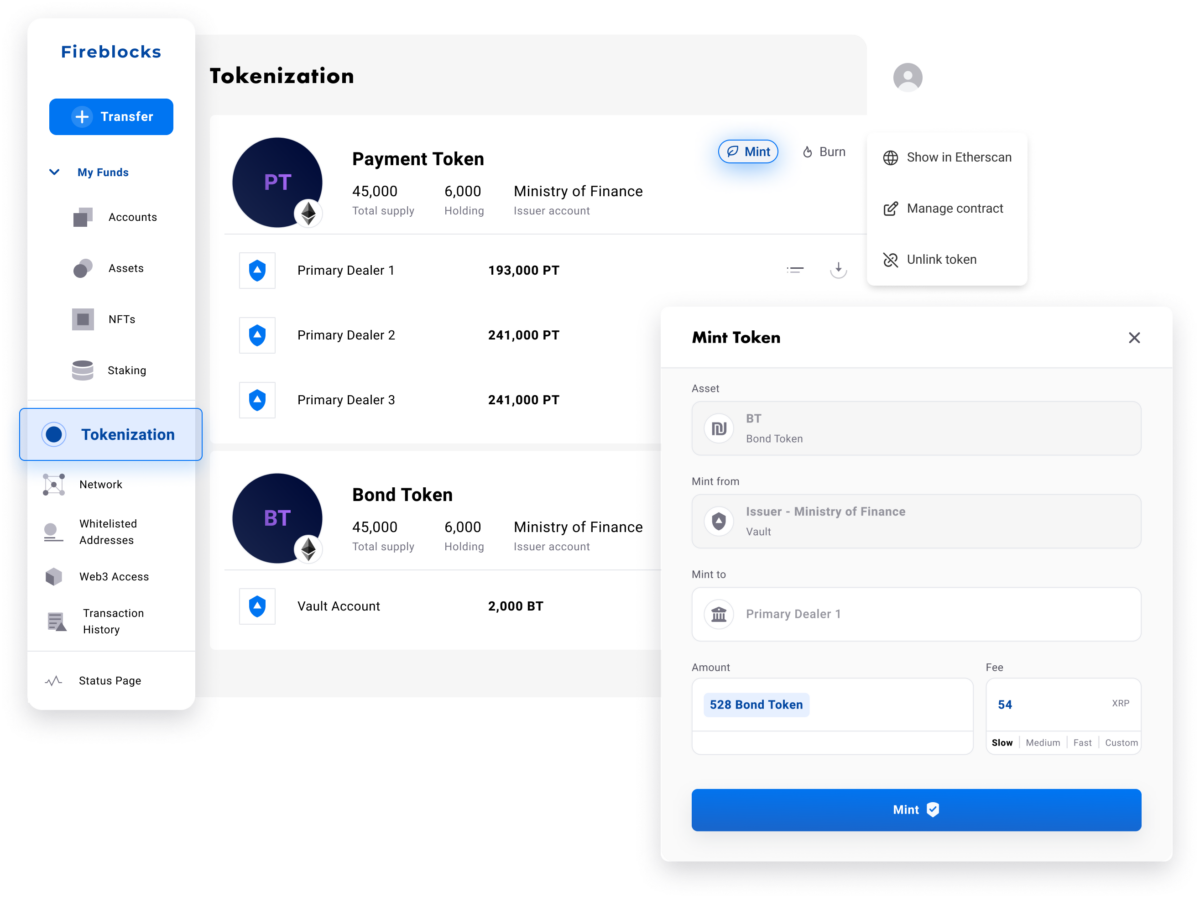
Fireblocks provides an end-to-end tokenization platform to securely mint, custody, and transfer tokenized assets and manage smart contracts. Connect with a network of market participants for token distribution, clearing, and settlement.